この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
問7:ダウンバーストの風速
図はダウンバーストの模式図である。
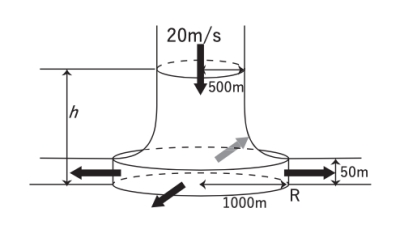
積乱雲からの下降流は円柱状に生じており、その下降流は地表付近に達するとほぼ水平に、地表面から高度50mまでの範囲で高さ方向に一様な風速で、図のように軸対称に広がるものとする。
高さhにおける円柱の半径を500m、下降流の速さを円柱内で一様に20m/sとする時、地表面近くで下降流の中心から1000m離れた地点Rにおける地表面から高さ50mまでの範囲の水平風速として最も適切なものを、次の①~⑤の中から1つ選べ。
ただし、定常状態を仮定し、高さhおよび地点Rの空気の密度は同じで、地表面との摩擦およびここに述べた以外の風は考慮しないものとする。
①20m/s
②40m/s
③50m/s
④60m/s
⑤80m/s
答えは③の50m/s!

まず情報を整理しますね。
求めるのは、地点Rの水平風速。
与えられた条件は
- 下降流は半径500mの円柱状
- 下降流の速度は20m/s
- 地点Rは中心から1000m離れている
- 地点Rの水平風は50mの厚みがある
とりあえず難しい条件は入ってないので、小学校の算数〜中学校の数学レベルの計算ができればOK!

地点Rでの風速を求める方法は、心太を想像してください!
1秒間に流れる空気の量を、面積と速度を使って求めます。
まず、半径500mの円を通る空気の速度は20m/sなので、1秒間に流れる空気の量は
500×500π×20m/s
=500×500×20π(m3/s)・・・①
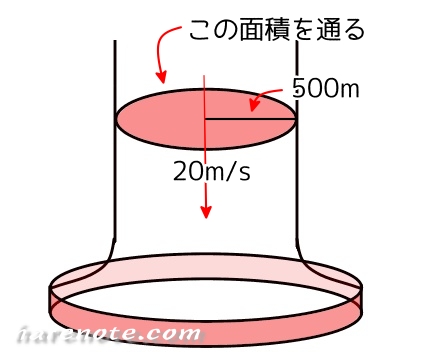
地点Rを通る時、空気の通る面積はこの側面の部分だから![]()
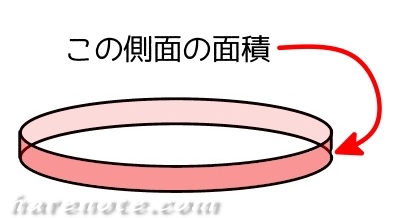
この側面の面積を求めるのは簡単♪
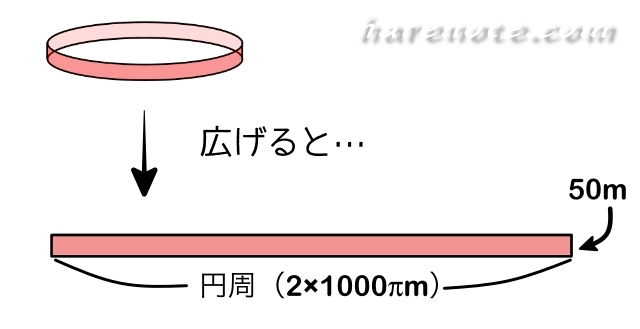
面積は円周×高さなので
2×1000×50π(m2)
風速はわからないのでVにして、1秒間に地点Rを通る空気の量は
2×1000×50Vπ(m3/s)・・・②
①と②は等しいので
500×500×20π(m3/s)= 2×1000×50Vπ(m3/s)
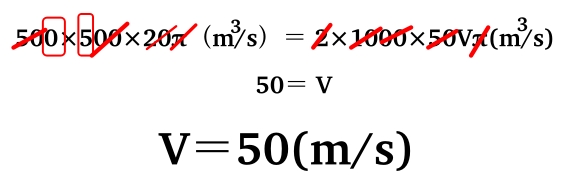

風速は50m/s!
ほとんど計算しなくても、答えが出ましたね。
他の解き方もありますよ〜(うちの息子の場合)
①の面積は→500×500π×m2=25×104m2
②の面積は→2×1000×50πm2=105m2
①:②=5:2
入り口①より出口②は2/5狭いから、5/2倍のスピードになると考えて・・・
20×5/2=50m/s

どっちの計算でも、答えは同じ!




