令和 5 年 1 月の第 59 回気象予報士試験の学科一般知識の問題を、
あなたが次に似たような問題を解く時、「ヒント」となるような内容を目指してます！！！
問１から順番に見る
この記事は、令和 5 年 1 月の第 59 回気象予報士試験の学科一般の問題と解答を持っている人向けの内容です。
※私個人の試験問題を解く時の思考例です。（気象業務支援センターとは関係ございません。）
もし第 59 回気象予報士試験の学科一般の問題と解答を持っていなければ、まずこちらでダウンロードしてください。
＼ まずはダウンロード！ ／
問1：気温の鉛直分布（大気の鉛直構造）
地球大気の平均的な気温の高度分布について述べた次の文（a）〜（c）の正誤の組み合わせとして正しいものを、下記の①〜⑤の中から1つ選べ。
（a）中間圏では、気温は高度が上がるとともに低下し、中間圏界面で極小となっている。
（b）成層圏では、オゾンが太陽からの紫外線を吸収して大気を加熱しており、オゾンの数密度が極大となる高度で気温も極大となっている。
（c）対流圏の気温減率は、放射や対流など様々な過程が関わり決まっているため、放射収支のみを考慮した計算から求められる気温減率よりも大きくなっている。
③ （a）正,（b）誤,（c）誤
鉛直方向の気温分布についての問題ですね。
基礎中の基礎の内容なので、秒で解いてやってください！
中間圏は高度が上がるとともに気温が低下し、中間圏海面付近で最も気温が低くなります。
だから（a）は正しい！
成層圏ではオゾンが紫外線を吸収して大気を加熱しているのはその通り…なんですが
気温の極大はオゾンの数密度が極大になる高度ではありません。
オゾンの数密度が極大となるのは成層圏中層。
気温が極大となるのは成層圏界面付近となります。
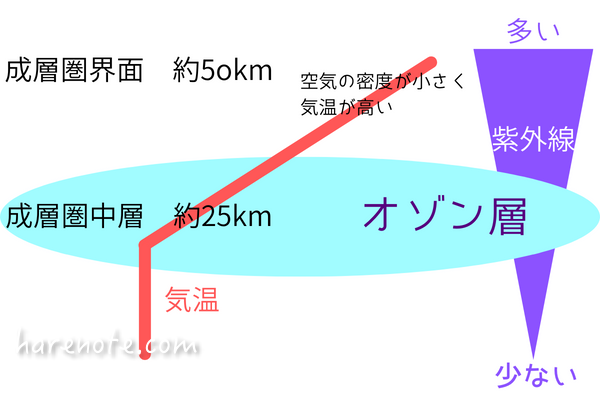
だから（b）の「成層圏では、オゾンが太陽からの紫外線を吸収して大気を加熱しており、オゾンの数密度が極大となる高度で気温も極大となっている。」は誤り！
対流圏は放射や対流などさまざまな過程が関わり、気温分布が決まっているわけですが・・・
もし！放射収支のみで気温分布が決まったら〜
地表面の暖かい空気が対流で上昇したりしないわけなので、高度が高くなるとともに、もっと気温は下がると考えられます。
タワマンの上層階はめっちゃ寒くて不人気になるかもw
そんなわけで、気温減率は放射収支のみより、対流がある方が小さくなります。
だから（c）は誤り!
「気象予報士講座」第 2 章【晴野が解いてみた】第59回の気象予報士試験の学科試験「予報業務に関する専門知識」はこちら
↓ ↓ ↓
その他の過去問を解いてみた記事はこちらからどうぞ
↓ ↓ ↓
