この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
問4:ステファン・ボルツマン〜ウイーンの変位則!
問題文
黒体放射について述べた次の文章の空欄(a)~(c)に入る適切な数式,語句および数値の 組み合わせを,下記の1~5の中から一つ選べ。
絶対温度T の黒体の単位面積から単位時間に放射されている波長別のエネルギー量を, すべての波長について積算した全エネルギー量は(a)に比例し,単位波長あたりの放射 強度が最も強くなる波長は T に(b)する。放射強度の最大値は,地球の放射平衡温度 255K の黒体放射では波長約 11μm のところにあり,太陽の表面温度約 6000K の黒体 放射では波長約(c)μm のところにある。
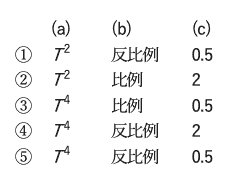
この問題は、黒体放射の問題。
この「放射強度は何の何乗に比例するのか?」という問題は、定番問題です。
I=σT4
- I:放射強度
- σ:ステファン・ボルツマン定数(5.67×10-8W/m2•K4)
- T:絶対温度

はれの
この問題では「全エネルギー量(a)に比例する」なので、「T4に比例する」ので①と②は除外。
(b)と(c)は、「ウイーンの変位則」で解ける問題です。
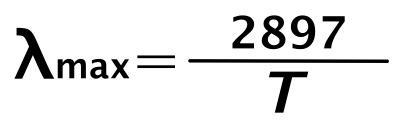
- λmax:最大となる波長(μm)
- T:絶対温度(K)
単位波長あたりの放射強度が最大となるのは、上の「ウイーンの変位則」の式から、Tに反比例するので、③は除外。
残りは④と⑤です。
Tに太陽の表面温度6000Kを代入すると
2897 ÷ 6000 = 0.48283333333……

はれの
答えは「0.5μm」!
※0.5μmの電磁波は、青〜緑あたりの可視光です♪
よって答えは⑤!




