この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
問5:降水過程の問題!
大気中の水蒸気が凝結して雲粒が生成され成⻑していく過程について述べた次の文 (a)〜(d)の正誤について,下記の1〜5の中から正しいものを一つ選べ。ただし,生成 される雲粒は純水の水滴とする。
(a) 表面張力のために,雲粒が小さいほど低い過飽和度で生成される。
(b) 雲粒が凝結過程によって成⻑するとき,周囲の空気の過飽和度が同じであれば,雲粒の半径が小さいほど一定時間内での半径の増加量が大きい。
(c) 雲粒の落下の終端速度は,雲粒の大きさによらない。
(d) 雲粒の併合過程では,雲内の雲粒の大きさが不ぞろいの場合よりも,大きさが一様な 場合の方が雲粒は速く成⻑する。

(a) 表面張力のために,雲粒が小さいほど低い過飽和度で生成される。
(b) 雲粒が凝結過程によって成⻑するとき,周囲の空気の過飽和度が同じであれば,雲粒の半径が小さいほど一定時間内での半径の増加量が大きい。
(c) 雲粒の落下の終端速度は,雲粒の大きさによらない。
(d) 雲粒の併合過程では,雲内の雲粒の大きさが不ぞろいの場合よりも,大きさが一様な 場合の方が雲粒は速く成⻑する。
純粋の水って設定もポイントですね。
水滴は表面張力のせいで、小さい水滴ほど成長するのにエネルギーが必要です。
つまり水滴が小さいほど過飽和度が大きくないと成長できないってこと。
だから(a)は間違い。
(b)は〇ですね。
過飽和度が同じ空気中で…大きい雲粒と小さい雲粒の成長する「半径の増加量」はどっちが大きくなるか?ですね。

雪玉をイメージするとわかりやすいですよ。
小さな雪玉と大きな雪玉を、雪の上で同じ時間転がした場合・・・
小さな雪玉の方が元サイズと比べたら、「増加量(割合)」は大きくなりますね。
では(c)の問題!
雲粒の落下の終端速度を求める式はこれ↓
mg=6πrηV
- m:水滴の質量
- g:重力加速度
- π:円周率
- r:水滴の半径
- η(エータ):粘性係数
- V:落下速度
もうこの式見ただけで、落下終端速度に水滴の大きさが絡んでいることはわかりますが〜
一応、目に見える数式にしちゃいますね。
mは水滴の質量なので、球の体積×密度から質量を求める式に変えちゃいます。↓
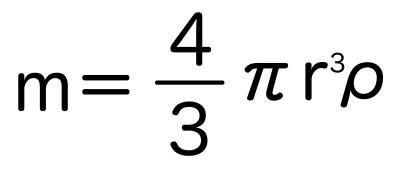
この水滴の質量を、さっきの終端速度を計算できる式にぶちこむと〜
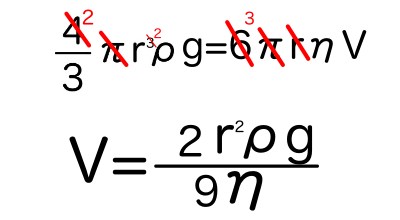

終端速度は「水滴の半径の2乗に比例する」ってはっきり言えますね!
だから(c)は間違い!
(d)は、雲粒→雨粒の併合過程の問題です。

これさっきの終端速度がめっちゃ関係してます!
「併合過程」は水滴の落下速度の違いで、水滴同士が衝突して併合し成長する過程のことです。
つまり、水滴同士の落下速度に差があることが大事。
水滴同士の落下速度に差がつくためには、水滴の大きさが違うことが必須!
というわけで、(d)も間違い!
水蒸気から雨粒ができる過程は、「一般気象学」や「よくわかる気象学」などの参考書を読み込んでおきましょう〜!




