この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
令和元年8月の第52回気象予報士試験の学科一般の問題を、晴野(はれの)だったらこう解く!という考え方や解き方をまとめています。
あなたが次に似たような問題を解く時、「ヒント」となるような内容を目指してます!!!

この記事は、令和元年8月の第52回気象予報士試験の学科一般の問題と解答を持っている人向けの内容です。
※私個人の試験問題を解く時の思考例です。(気象業務支援センターとは関係ございません。)
もし第53回気象予報士試験の学科一般の問題と解答を持っていなければ、まずこちらでダウンロードしてください。![]()
\ まずはダウンロード! /
問1:大気の構造についての問題
ここ数年、学科・一般の問1は、「大気の構造」についての問題が出てますね。
第53回の学科・一般も問1に「大気の構造」の問題が出てたので、しっかり理解して覚えておきましょう!
④ (a)低い, (b)高い, (c)200, (d)紫外線による光解離
まず(a)と(b)は対流圏・成層圏・中間圏・熱圏の温度分布は基礎中の基礎知識なので、絶対覚えてね。![]()
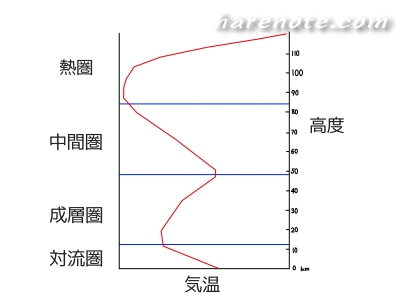
| 対流圏では上空へ行くほど | 気温が下がる |
| 成層圏では上空へ行くほど | 気温が上がる |
| 中間圏では上空へ行くほど | 気温が下がる |
| 熱圏では上空へ行くほど | 気温が上がる |
(c)の気圧についての問題は、あまり注目されないところで「ここが出るんか?!」って思いました。
でも基本的なことを知ってたら解けちゃいます。

問題では「成層圏の最下層の気圧」を問われているので、答えは「対流圏界面付近の気圧」に近いですよね!
例えば馴染みのある高層天気図の300hPa面の天気図は、高度9000mくらいの天気図です。
対流圏界面の高度は8000m〜16000m。
ということは〜
選択肢にある「10hPa」は明らかにおかしくて、約200hPaが正解!
表にしておきます〜
| 大気圏各層 | 最下層の気圧 |
|---|---|
| 熱圏 | 約0.01hPa |
| 中間圏 | 約1hPa |
| 成層圏 | 約200hPa |
| 対流圏 | 約1000hPa |
続いて(d)!
問題に登場した用語は、この3つ。
- 準2年周期振動
- 紫外線による光電離
- ブリューワー・ドブソン循環
それぞれ、どこのどんな現象のことか表にまとめます。
| 現象の名前 | どこで起こる? | どんな現象? |
|---|---|---|
| 準2年周期振動 | 赤道付近の成層圏下部 | 26ヶ月で東風と西風が交互に吹く現象 |
| 紫外線による光電離 | 熱圏 | 太陽からの紫外線(波長0.1μm以下)が原子から電子を叩き出して原子がイオン化する現象 |
| ブリューワー・ドブソン循環 | 下層成層圏 | 下層成層圏の子午面で見られる、低緯度から高緯度への風が吹いている現象 |
中層大気の子午面の流れを表した模式図、覚えてますか?
「一般気象学(第2版)」 p254にある図9.4です。
ブリューワー・ドブソン循環って、ブリューワーさんとドブソンさんの研究でわかった循環だからの名前ですが・・・
もっとわかりやすい名前だったらなぁ…と思わずにはいられません〜

そんなわけで、答えは④でしたね。






