この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
問14:予測精度について
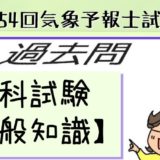
表は、ある地点の1日~10日の日毎の最高気温の実況値、モデルXおよびモデルYによる最高気温の予測値を示したものである。
予測値の検証について述べた次の文(a)~(c)の正誤の組み合わせとして正しいものを、下記の①~⑤の中から1つ選べ。
(a)実況で夏日になった日のみを抜き出して、最高気温予測の系統的な偏りを平均誤差(ME)により求めると、モデルXの予測値は実況値より低めであった。
(b)10日間の最高気温予測の精度を2乗平均平方根誤差(RMSE)により求めると、モデルYの方がモデルXより予測精度がよい。
(c)実況で真夏日になった日のみを抜き出して最高気温予測の精度を2乗平均平方根誤差(RMSE)により求めると、モデルXの方がモデルYより予測精度がよい。

答えは・・・①! (a)(b)(c)すべて正しい!

夏日、真夏日の気温は覚えてるよね?
25℃と30℃だよ!
夏日とは、日最高気温が25度以上の日のこと。
平均誤差(ME)は、「予報値」ー「実況値」を足したものを平均したものです。
夏日になった日のみ抜き出してモデルXの平均誤差を求めると・・・
(-3)+(-1)+(-1)+(-1)+1+2 = -3
-3 ÷ 6 = -0.5
平均誤差がマイナスなので、実況値より低いってことですね。
だから(a)実況で夏日になった日のみを抜き出して、最高気温予測の系統的な偏りを平均誤差(ME)により求めると、モデルXの予測値は実況値より低めであった。」は正しい!
2乗平均平方根誤差(RMSE)とは、「予測値」ー「実況値」を二乗したものを足して平均したものの平方根です。

この問題は、2乗平均平方根誤差を求めることが目的ではなく、XとYの比較ができればOKです。
だから誤差を二乗したものを足すだけで比較できます。
- モデルX→誤差の二乗を足すと23
- モデルY→誤差の二乗を足すと19
値が小さい方が予測精度が良いので、モデルYの方が予測精度は良いですね!
だから(b)の「10日間の最高気温予測の精度を2乗平均平方根誤差(RMSE)により求めると、モデルYの方がモデルXより予測精度がよい。」は正しい!

実際に足し算すらしなくても・・・パッと見モデルYの方が精度が良さそうなので、試験本番では計算は最後にしましょうね。
真夏日は最高気温が30℃以上。
- モデルX→誤差の二乗を足すと8
- モデルY→誤差の二乗を足すと13
値が小さい方が予測精度が良いので、モデルXの方が予測精度は良いですね!
というわけで(c)の「実況で真夏日になった日のみを抜き出して最高気温予測の精度を2乗平均平方根誤差(RMSE)により求めると、モデルXの方がモデルYより予測精度がよい。」は正しい!
318, 319ページ