問 5:水滴の併合過程
雲の中の水滴の併合過程による成長について述べた次の文章の空欄(a)~(c)に入る数式と語句の組み合わせとして正しいものを、下記の①~⑤の中から1つ選べ。ただし、水滴はすべて球体であり、小さな水滴の落下速度は0(ゼロ)とする。
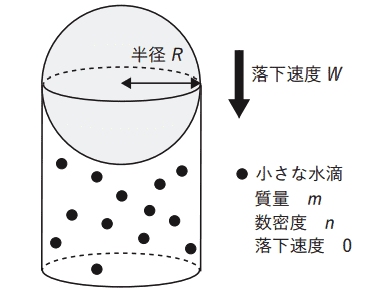
図のように、質量mの小さな水滴が単位体積当たりの数密度nで一様に分布している雲の中を、小さな水滴よりも十分に大きい半径 Rの水滴が鉛直下向きに速さ Wで落下している。
大きな水滴が、通過する空間内のすべての小さな水滴を併合するとしたとき、大きな水滴の質量の単位時間あたりの増加量は(a)である。
質量の増加に伴い、大きな水滴の半径が表面全体(表面積 4πR2)で一様に増加するとすれば、単位時間の半径の増加量は(b) に比例する。
このとき、Wが R1/2に比例するとすれば、水滴が大きくなるとともに単位時間の半径の増加量は(c) なる。
④ (a)πmnR2W,(b)W,(c)大きく
小さな水滴の質量:m
小さな水滴の数密度:n
大きな水滴の半径:R
大きな水滴の落下速度:W
なんだか沢山アルファベットが出てきて頭がパンクしそうなので、適当に単位をつけて頭を整理します。
小さな水滴の質量:m(g)
小さな水滴の数密度:n(個/m3)
大きな水滴の半径:R(m)
大きな水滴の落下速度:W(m/s)
↑単位はわかりやすく単純に決めただけなので、ツッコミは受け付けません。
それで、です・・・
大きな水滴の質量の、単位時間あたり増加量を考えます。
大きな水滴が単位時間あたり(例えば1秒)に落下する高さ(距離)はW(m)です。
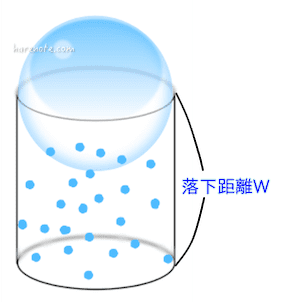
底面の面積「πR2」で高さ「W」の円柱の体積は、「πR2W」。
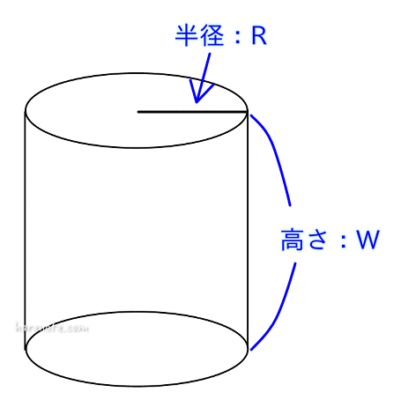
この円柱の中にある小さな水滴は「n×πR2W個」。
これらの小さな水滴の質量は「m×n×πR2W」。
単位を整えると納得できるね。↓
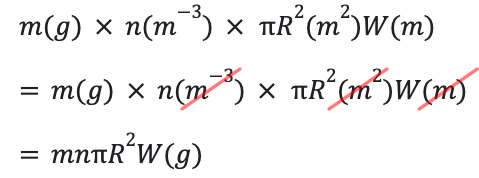
つまり、大きな水滴の、単位時間あたりの質量の増加量は(a)「πmnR2W」。

解答は③④⑤に絞られました。
次に、大きな水滴の質量が増加する時、大きな水滴の半径Rは何に比例するか。
選択肢は「W/R」,「W」,「WR」。
元々の大きな水滴の質量は、水なので体積と同じと考えて、「4πR3/3」。
単位時間あたりに増加する質量は「πmnR2W」。
今は何に比例するのかだけ考えればいいので、こんな感じで簡単に式にして・・・
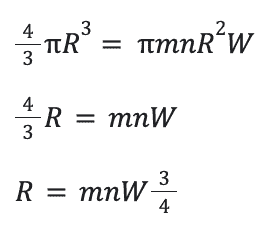

こんな感じで選択肢「W/R」,「W」,「WR」の中で当てはまるのは「W」なので
答えは④になります。
(c)は確認するだけ。
R1/2 は、二乗すれば R になるという意味なので、Wが R1/2に比例するということは、こういうこと↓
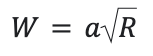
水滴が大きくなるとともに単位時間の半径の増加量は(c)「大きく」 なりますね。
その他の過去問を解いてみた記事はこちらからどうぞ
↓ ↓ ↓





