この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
気象予報士試験・学科試験「予報業務に関する専門知識」の過去問の中から、最も高頻度で出題される科目「予報」についての問題のみを集めました。
今回は第50回と第49回の試験に出題された問題をまとめています。

ここでは気象予報士試験の学科試験・専門知識で出題される科目「予報」についての過去問(第50回の試験〜第49回の試験)をまとめておさらいできるようになっています。
「予報」に関する問題は、毎回4〜6問出題されます!
だからこの科目の過去問は、ぜひ集中してインプットしていきたいところ。
過去問を通して似たような問題を繰り返し解くことで、学習効率も上がりますよ〜

過去に出題された「予報」に関るる問題をまとめて解くことで、予報に関する知識を更に深めましょう!
※「予報」についてのその他の試験回の過去問まとめはこちらからどうぞ![]()
【学科・専門】「予報」に関する過去問&解説総まとめ!
第50回出題:大気海洋結合モデルについて
気象庁が運用している大気海洋結合モデルに関する次の文(a)〜(c)の下線部の正誤の 組み合わせとして正しいものを,下記の1〜5の中から一つ選べ。
(a) 予測期間が⻑期にわたると,大気と海洋の相互作用が無視できなくなるため, 1 か月を超える予測には大気海洋結合モデルを用いている。
(b) 大気海洋結合モデルでは,大気と海洋の間の熱や水蒸気や運動量の輸送を通じた 大気の温度や湿度の変化とともに,海洋の水温や海流などの変化も予測する。
(c) 大気海洋結合モデルの予測では,アンサンブル予報の手法が用いられている。

① (a)正, (b)正, (c)正

大気海洋結合モデルについて、こちらでザックリと紹介してます。 ▶︎▶︎▶︎ 大気海洋結合モデル(用語集)
1ヶ月を超える予報には、エルニーニョ 現象やラニーニャ 現象などの海洋の様子も反映させたモデルが必要になります。
だから「(a) 予測期間が⻑期にわたると,大気と海洋の相互作用が無視できなくなるため, 1 か月を超える予測には大気海洋結合モデルを用いている。」は正しい!
大気海洋結合モデルは、
- 大気の温度・湿度の変化
- 海洋の水温の変化
- 海流の変化
を予測します。
だから「(b) 大気海洋結合モデルでは,大気と海洋の間の熱や水蒸気や運動量の輸送を通じた 大気の温度や湿度の変化とともに,海洋の水温や海流などの変化も予測する。」は正しい!
1か月を越える予報には、「大気海洋結合モデル」を用いた「季節アンサンブル予報システム」が使用されているので・・・
「(c) 大気海洋結合モデルの予測では,アンサンブル予報の手法が用いられている。」は正しい!

ポイントをまとめよう
| 1 か月を超える予測に使われているシステムは? | 「大気海洋結合モデル」を用いた「季節アンサンブル予報システム」 |
| 大気海洋結合モデルで予測するもの | 大気の温度・湿度の変化 海洋の水温 海流 |
気象庁のこのページ、プリントしてノートに貼ってもいいと思います!
▶︎▶︎▶︎「数値予報モデルの種類(気象庁)」
第50回出題:全球モデルについて
気象庁が明後日までの天気予報に使用している全球モデルについて説明した次の文(a) 〜(c)の正誤の組み合わせとして正しいものを,下記の1〜5の中から一つ選べ。
(a) 全球モデルでは,静力学平衡を仮定した近似を使っている。
(b) 全球モデルの水平格子間隔は約 20km であり,それより小さなスケールの現象である積雲や乱流等の効果は考慮されていない。
(c) 全球モデルの予測値は,メソモデルによる予測やその初期値を作るための客観解析 における境界条件としても用いられる。そのため,全球モデルが改良されその予測 特性が変化すると,メソモデルの予測特性も変化することがある。

② (a)正, (b)誤, (c)正
全球モデルは「プリミティブモデル」であり
「プリミティブモデル」は、数値予報で使われる物理学の方程式で、鉛直方向の運動方程式に静水圧平衡(静力学平衡)近似を用いる数値予報モデルのことなので・・・
「(a) 全球モデルでは,静力学平衡を仮定した近似を使っている。」は正しい!
問題文にある「積雲や乱流等の効果」っていうのは、全球モデル(GSM)で扱う物理過程に「積雲対流パラメタリゼーション」はあるんか?ってことですよね!

GSMは直接積雲を格子点の値として扱えないけど、パラメタリゼーションとして積雲や乱流の効果を見積もっています。
だから「(b) 全球モデルの水平格子間隔は約 20km であり,それより小さなスケールの現象である積雲や乱流等の効果は考慮されていない。」は誤り!
メソモデル(MSM)は境界条件として全球モデル(GSM)を用いています。
だから全球モデル(GSM)が改良されてバイアスが軽減すれば、メソモデル(MSM)にも同じような影響は出るのです。
というわけで「(c) 全球モデルの予測値は,メソモデルによる予測やその初期値を作るための客観解析 における境界条件としても用いられる。そのため,全球モデルが改良されその予測 特性が変化すると,メソモデルの予測特性も変化することがある。」は正しい!

ポイントをまとめよう
- 全球モデル(GSM)はプリミティブモデルである。
- プリミティブモデルでは静力学平衡を仮定した近似を使っている。
- 格子点間隔より小さい現象については、パラメタリゼーションとして効果を見積もっている。
- メソモデル(MSM)は境界条件として全球モデル(GSM)を用いている。
- 境界条件として用いる親モデルの変化は、子モデルにも影響する。
| 出てきた用語 | 意味 |
|---|---|
| メソモデル(MSM) | 日本と日本の近海の大気を対象とする数値予報モデル。 |
| 全球モデル(GSM) | 地球全体の大気を対象とする数値予報モデル。 |
| プリミティブモデル | 鉛直方向の運動方程式に静力学平衡を仮定した近似を用いている数値予報モデル。→GSMはプリミティブモデル。 |
第50回出題:降水確率予報の精度評価について
コストロスモデルの考えに基づいた降水確率予報の利用に関する次の文章の空欄(a)〜(c) に入る適切な数および数式の組み合わせを,下記の1〜5の中から一つ選べ。ただし,確率予報の信頼度は 100%であるものとする。
数値予報の確率情報の有効な利用方法として,ある大気現象による損失を防ぐために対 策を施した場合にかかる費用(コスト)と,何も対策を施さなかった場合に被る損失(ロス) の合計を基に,経済効果の観点からどのような対策を施すべきかを判断する方法がある。
今,降水対策を施す場合の 1 回あたりのコストを 100,対策を行わなかった場合の ロスを 500 とし,降水確率が A%である予報が 10 回出たものとする。
この 10 回の事例で降水対策を施した場合のコストの合計は$(a)$であり,降水対策 を全く施さなかった場合のロスの合計は$(b)$である。したがって,(c)$の場合に降水 対策を施すと,何も対策を施さなかった場合よりもコストとロスの合計が少なく,経 済効果が大きいと期待される。

⑤ (a)1000, (b)50 × A, (c)A > 20
降水対策1回あたりのコストが100で、10回対策したので・・・
コストは 100×10回=1000 ですね!
対策を行わなかった場合のロスは500で、対策を行わなかったのは10回。
降水確率はA%なので(予報100回中A回、1ミリ以上の降水があるってこと)
ロスは 500 × 10 × ( A/100 ) = 50A ですね!
(a)と(b)の答えから、降水確率が20%だったら、コストとロスの値が同じになりますよね。
※根拠
50A = 1000
A = 1000/50 = 20
ということは、降水確率が20%以上だと、ロスの方が大きくなっちゃうので、コストをかけてでも対策を施す方が経済効果が大きいです。
だから経済効果が期待されるのは(c)A > 20 になる時です!

ポイントをまとめよう
- ロス(L):特定の天気現象によって起こる損失
- コスト(C):特定の天気現象によって起こる損失を防ぐために施す対策費用
| 現象 | 有り | 無し |
|---|---|---|
| 対策有り | C(100) | C(100) |
| 対策無し | L(500) | 0 |
| 現象 | 有り | 無し |
|---|---|---|
| 対策有り | C(1000) | C(1000) |
| 対策無し | L(50A) | 0 |
参考になったのは…イラスト図解よくわかる気象学・専門知識編(P320)
第49回出題:数値予報の改良とその効果
気象庁の数値予報の改良とその効果について述べた次の文(a)〜(c)の正誤の組み合わ せとして正しいものを,下記の1〜5の中から一つ選べ。
(a) 少しずつ異なる初期値を多数用意して多数の予報を行うアンサンブル予報の手法 を導入し,予報結果のアンサンブル平均を取ることにより,気温や高度場の予報の 系統的な誤差が減少した。
(b) 客観解析に 4 次元変分法を導入することにより,数値予報の初期時刻と異なる時 刻に観測されたデータを効果的に利用できるようになった。
(c) 積雲の効果をパラメタリゼーションにより数値予報モデルに取り込むことで,個々 の積雲の発達,衰弱を予測できるようになった。

③ (a)誤, (b)正, (c)誤
アンサンブル予報は初期値の異なる多数の予想結果を平均する予報で、散らばった予想の平均を予想結果とするものです。
でもそのアンサンブル予報って系統的誤差って減らせるの?ってとこがポイントになります。
系統的誤差はモデルの地形などの癖のことです。

いつも決まった癖があるなら、過去の情報を使ってそれを減らせるわけですが・・・
アンサンブル予報は系統的誤差を減らすために平均をとるのではなく、初期値の違いで差が広がっていく予測値の平均をとるものです。
だから系統的誤差を減らすのは難しいので…
(a)の「 少しずつ異なる初期値を多数用意して多数の予報を行うアンサンブル予報の手法 を導入し,予報結果のアンサンブル平均を取ることにより,気温や高度場の予報の 系統的な誤差が減少した。」は誤り!
客観解析に四次元変分法を導入したおかげで、異なる時刻に観測されたデータを効果的に利用できるようになったか?って問題です。
ええ、そりゃあ時間データも含む四次元変分法では、三次元変分法より効果的になったので「(b) 客観解析に 4 次元変分法を導入することにより,数値予報の初期時刻と異なる時 刻に観測されたデータを効果的に利用できるようになった。」は正しい!

観測値の補正は定時観測だけじゃなく、定時の前後の時刻の値も時間軸に重みを持たせて初期値を補正することができるから・・・
予報値の精度は上がるはずだよね!
▶▶︎▶︎︎四次元変分法(用語解説)
数値予報に積雲の効果をパラメタリゼーションで取り込むと・・・「個々 の積雲の発達,衰弱を予測できるようになった」???
そんなわけないですよね!
そもそもパラメタリゼーションってのは、モデルの格子点の間隔以下のスケールの小さな現象の情報を考慮するためのものです。
スケールの小さな積雲などの現象は、そのまんま格子点の値にはできないけど、無視したら天気予報できないよね!ってとこからの〜
じゃあその小さな物理効果をなんとか数値予報に取り込みたい!ってか取り込むぞ!というのがパラメタリゼーションね。

だからパラメタリゼーションは、小さな現象の物理効果を考慮するものであって、個々のの積雲が「発達するよ〜」 or 「衰弱しまっせ〜」と予想するものではないわけです。
だから「(c) 積雲の効果をパラメタリゼーションにより数値予報モデルに取り込むことで,個々 の積雲の発達,衰弱を予測できるようになった。」は誤り!
▶▶︎▶︎︎パラメタリゼーション

ポイントをまとめよう
| アンサンブル予報って何のためのもの? | 初期値の不確実性が要因となるランダム誤差を減らすためのもの。 (結果を統計的に解釈することで、単独予報より予報誤差を減らせる。) |
| 出てきた用語 | 意味 |
|---|---|
| 四次元変分法 | 客観解析で格子点の値を決定する方法で、非定時の値も解析に使う。 定時の前後の時刻の値も時間軸に重みを持たせて初期値を補正することができる。 |
| パラメタリゼーション | モデルの格子点の間隔以下のスケールの小さな現象の物理的効果を表現して、数値モデルなどの方程式に加えること |
第49回出題:数値予報プロダクトの利用
気象庁が作成している数値予報プロダクトの利用にあたって留意すべき事項について 述べた次の文(a)〜(c)の正誤の組み合わせとして正しいものを,下記の1〜5の中から一 つ選べ。
(a) 水平スケールの大きな現象ほど,数値予報により予測が可能な時間は短い。
(b) メソモデルの予報結果は,予報領域の境界を通じて全球モデルの予報結果の影響を受けるが,その影響は予報時間が⻑くなるほど小さくなっていく。
(c) 週間アンサンブル予報結果のスプレッドが大きい場合は,小さい場合に比べて一般 に予報の精度が低い。

④ (a)誤, (b)誤, (c)正
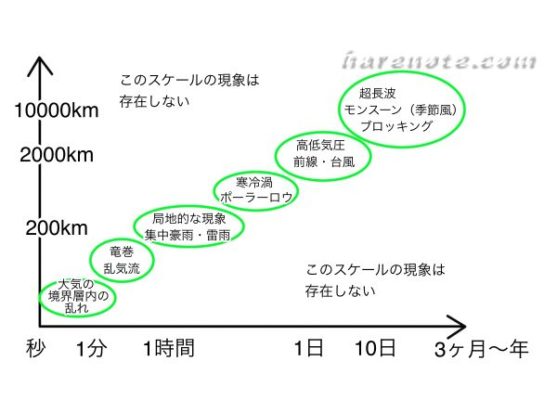
水平スケールの大きな現象ほど、寿命が長いので・・・
(a)の「 水平スケールの大きな現象ほど,数値予報により予測が可能な時間は短い。」は誤り!
メソモデルの予報結果は、予報領域の境界を通じて全球モデルの予報結果の影響を受けます。
この境界での全球モデルからの影響は、予報時間が長くなるほど・・・
小さくなるか?
いや小さくならんでしょ!
だから(b) の「メソモデルの予報結果は,予報領域の境界を通じて全球モデルの予報結果の影響を受けるが,その影響は予報時間が⻑くなるほど小さくなっていく。」は誤り!
週間アンサンブル予報結果のスプレッドが大きい場合…
スプレッドが小さい場合に比べて、予報の精度は低くなります。
イメージで理解しちゃってください!![]()
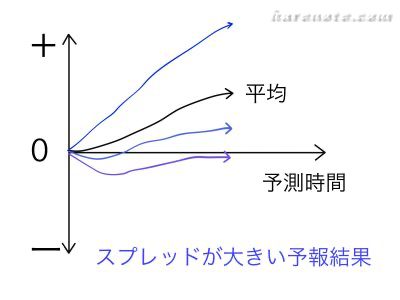
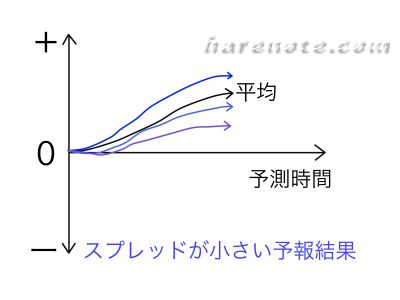
結果として出てくる平均値が同じでも、スプレッドが大きいのとスプレッドが小さいのとでは、予報結果への精度が違いますよね!
だから(c) の「週間アンサンブル予報結果のスプレッドが大きい場合は,小さい場合に比べて一般 に予報の精度が低い。」は正しい!

ポイントをまとめよう
| 現象の水平スケールと時間スケール | 正の相関関係にある |
| メソモデルの境界条件として用いられる全球モデルからの影響と時間経過 | 時間が経過しても全球モデルからの影響が小さくなるものではない。 |
| アンサンブル予報における個々の予想結果のスプレッドはで精度が良いのは? | スプレッドが小さい方が予報の精度が良い。 |
第49回出題:ガイダンスによる数値予報の誤差の軽減
気象庁の天気予報ガイダンスによる数値予報の誤差の軽減について述べた次の文 (a)〜(c)の正誤の組み合わせとして正しいものを,下記の1〜5の中から一つ選べ。
(a) 気温ガイダンスにより,数値予報で予想できない局地的降水によって生じる地上 気温の誤差を軽減できる。
(b) 降水量ガイダンスにより,数値予報モデルに組み込まれている地形と実際の地形 の違いによって生じる降水量の誤差を軽減できる。
(c) 風ガイダンスにより,寒冷前線の通過のタイミングが数値予報の予想と異なること によって生じる風向の時間変化の誤差を軽減できる。

⑤ (a)誤, (b)正, (c)誤
そもそもガイダンスは…
- 系統的誤差→軽減できる。
- ランダム誤差→軽減することができない。
そして「局地降水による地上気温の変化」は、系統的誤差とは言えないですね…。

どっちかって言うと「ランダム誤差」ですね〜。
だから(a) の「気温ガイダンスにより,数値予報で予想できない局地的降水によって生じる地上 気温の誤差を軽減できる。」は誤り!

「地形と実際の地形の違いによって生じる降水量の誤差」は、まさしく「系統的誤差」ですね!
だから(b)の「 降水量ガイダンスにより,数値予報モデルに組み込まれている地形と実際の地形 の違いによって生じる降水量の誤差を軽減できる。」は正しい!
前線の位置が予想と実際とでずれちゃう場合は、パターンとして毎回あるわけではなく、「ランダム誤差」の代表です!
だから(c)の「 風ガイダンスにより,寒冷前線の通過のタイミングが数値予報の予想と異なることによって生じる風向の時間変化の誤差を軽減できる。」は誤り!

ポイントをまとめよう
| 系統的誤差 | ランダム誤差 |
|---|---|
| モデルと実際の地形の違いによって生じる誤差 | 局地的降水によって生じた気温の誤差 |
| 予報モデルのクセによる誤差 | 予想と実際の前線の位置が違うことで生じる誤差 |
気象予報士試験第50回・第49回で出題された「予報」についての問題をお伝えしました。
次は第48回以前に出題された「予報」についての問題もまとめるので、今しばらくお待ちください〜(о´∀`о)
気象予報士試験第54回・第53回で出題された「予報」についての問題はこちら![]()
気象予報士試験第52回・第51回で出題された「予報」についての問題はこちら![]()






